Maxwell Equations in the Schwarzchild Space
Renan Cabrera
cabrer7@uwindsor.ca
Initializations
In[1]:=
![]()
We set base indices for relativity, and define tensor shortcuts for the coordinates x, the 4-current J, the electric field ξ, the metric tensor g, the Maxwell tensor F, the Kronecker δ, and the Christoffel symbols Γ.
In[2]:=
![]()
![]()
![]()
![]()
The metric tensor of this space is given by the components of the following matrix:
In[6]:=
![]()
![]()
![]()
Out[7]//MatrixForm=
![( {{-1 + (2 M)/r, 0, 0, 0}, {0, 1/(1 - (2 M)/r), 0, 0}, {0, 0, r^2, 0}, {0, 0, 0, r^2 Sin[θ]^2}} )](HTMLFiles/index_9.gif)
Out[8]//MatrixForm=
![( {{-1 + (2 M)/x_1^1, 0, 0, 0}, {0, 1/(1 - (2 M)/x_1^1), 0, 0}, {0, 0, (x_1^1)^2, 0}, {0, 0, 0, Sin[x_2^2]^2 (x_1^1)^2}} )](HTMLFiles/index_10.gif)
Setting the values to the metric tensor and Christoffel symbol.
In[9]:=
![]()
![]()
Non Homogeneous Maxwell Equations
The following closed cell contains the Tensorial code to derive the equation for the radial electric field in the Schwarzchild metric. Select the cell and evaluate to obtain the derivation. (Select the cell and use Alt C R C to see the code, or use Menu → Cell → Cell Properties → Cell Open.)
![]()
Out[13]=
![]()
![]()
Out[15]=
![]()
![]()
Out[17]=
![]()
![]()
Out[19]=
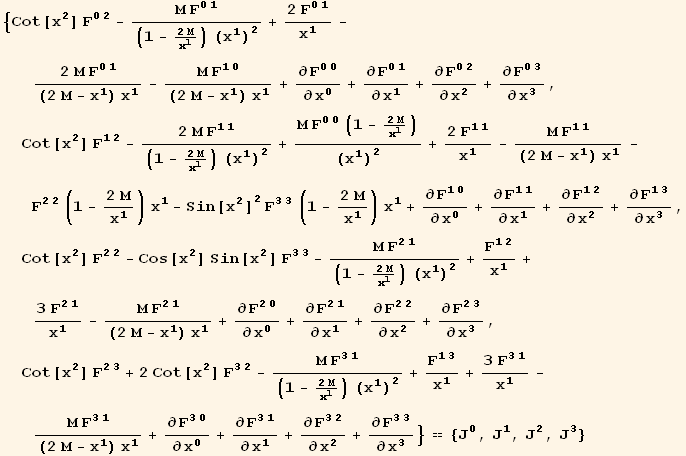
![]()
Out[21]=
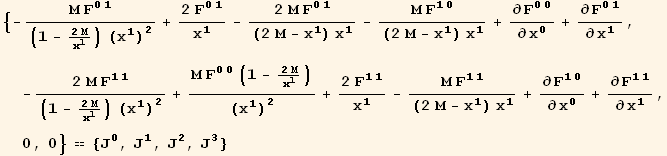
![]()
Out[23]=
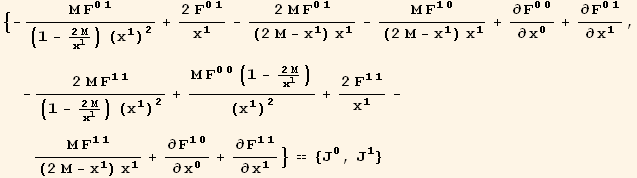
![]()
Out[25]=
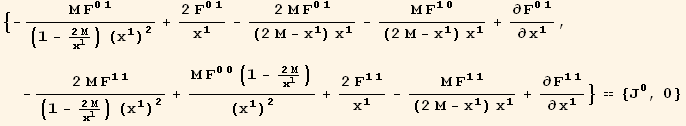
![]()
Out[27]=
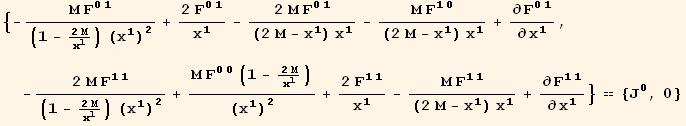
![]()
Out[30]=
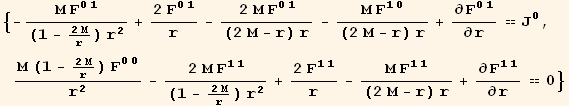
![]()
Out[32]=
![]()
Out[33]=
![]()
We obtain a single equation for the radial electric field.
This result can be obtained by a second method. Taking the Divergence of the electric field ξ, and applying similar conditions.
In[34]:=
![]()
![]()
![]()
![]()
![]()
Out[34]=
![]()
Out[35]=
![]()
Out[36]=
![]()
Out[37]=
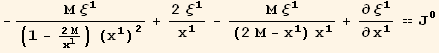
Out[38]=
![]()
Where we obtain the same equation provided that ![]() =
= ![]() , which is according the definition of the Maxwell tensor.
, which is according the definition of the Maxwell tensor.
| Created by Mathematica (November 22, 2007) |